• You are here:  
  • Home
  • Materials

Details
Materials & Properties
Hits: 607

The shear modulus, also known as the modulus of rigidity, is a measure of the stiffness of a material in response to shear stress. It is defined as the ratio of the applied shear stress to the corresponding shear strain within the elastic range of the material. Shear stress is defined as the force applied to a material in a direction perpendicular to the surface, and shear strain is the resulting deformation of the material in response to the applied shear stress.

The shear modulus of a material is an important property that determines how much a material will deform under shear stress. Materials with a high shear modulus are generally stiffer and stronger in response to shear stress, and they tend to deform less under shear load. Conversely, materials with a low shear modulus are more flexible and deform more easily under shear load.

The shear modulus of a material can be measured using a variety of techniques, including torsion testing and simple shear testing. The shear modulus of a material is often used to predict the behavior of a structure under shear load, and it is an important consideration in the design of many engineering systems.

The shear modulus is typically measured in units of pressure, such as gigapascals (GPa) or megapascals (MPa). It is important to note that the shear modulus of a material can vary depending on the temperature, humidity, and other environmental conditions. In addition, the shear modulus can vary depending on the type of loading that is applied to the material, such as tensile, compressive, or shear stress. Therefore, it is important to carefully control the test conditions when measuring the shear modulus of a material.

HOW IS SHEAR MODULUS CALCULATED?

The shear modulus of a material can be calculated using the following equation:

Shear modulus = shear stress / shear strain

where shear stress is the force applied to the material in a direction perpendicular to the surface, and shear strain is the resulting deformation of the material. The shear modulus is typically measured in units of pressure, such as gigapascals (GPa) or megapascals (MPa).

To measure the shear modulus of a material, a sample of the material is subjected to a shear load, and the resulting shear stress and strain are measured. The shear modulus can then be calculated by dividing the shear stress by the shear strain.

In practice, the shear modulus of a material is usually determined using a standard test procedure, such as the torsion test or the simple shear test. These tests involve applying a shear load to a sample of the material and measuring the resulting deformation. The shear modulus can then be calculated from the measured shear stress and strain values.

It is important to note that the shear modulus of a material can vary depending on the temperature, humidity, and other environmental conditions. In addition, the shear modulus can vary depending on the type of loading that is applied to the material, such as tensile, compressive, or shear stress. Therefore, it is important to carefully control the test conditions when measuring the shear modulus of a material.

HOW CAN SHEAR MODULUS BE IMPROVED?

There are several ways to improve the shear modulus of a material:

  1. Use high-modulus fibers: The shear modulus of a composite material is largely determined by the modulus of the fibers used in the material. Using high-modulus fibers, such as carbon fibers or high-strength fibers, can significantly increase the shear modulus of the composite material.

  2. Increase the fiber volume fraction: The shear modulus of a composite material also depends on the volume fraction of fibers in the material. Increasing the fiber volume fraction can increase the shear modulus of the composite material.

  3. Use a high-modulus matrix: The matrix material that surrounds the fibers in a composite material can also affect the shear modulus of the material. Using a matrix material with a high modulus, such as an epoxy resin or a polyimide, can increase the shear modulus of the composite material.

  4. Use a unidirectional fiber orientation: The orientation of the fibers in a composite material can also affect the shear modulus. Using a unidirectional fiber orientation, where the fibers are aligned in a single direction, can increase the shear modulus of the composite material.

  5. Use a hybrid fiber configuration: Using a hybrid fiber configuration, where different types of fibers are used in different directions, can also improve the shear modulus of a composite material.

  6. Improve the fiber-matrix interface: The strength of the fiber-matrix interface can also affect the shear modulus of a composite material. Improving the fiber-matrix interface, such as by using a compatible matrix material or by optimizing the fiber treatment process, can increase the shear modulus of the composite material.

 

 

 

Details
Materials & Properties
Hits: 599

Elastic modulus, also known as Young's modulus, is a measure of the stiffness of a material. It is defined as the ratio of the applied stress to the corresponding strain within the elastic range of the material. Stress is defined as the force applied to a material per unit area, and strain is the resulting deformation of the material in response to the applied stress.

The elastic modulus of a material is an important property that determines how much a material will deform under a given load. Materials with a high elastic modulus are generally stiffer and stronger, and they tend to deform less under load. Conversely, materials with a low elastic modulus are more flexible and deform more easily under load.

The elastic modulus of a material can be measured using a variety of techniques, including tensile testing, compression testing, and bending testing. The elastic modulus of a material is often used to predict the behavior of a structure under load, and it is an important consideration in the design of many engineering systems.

There are several different types of elastic modulus, including the Young's modulus, the shear modulus, and the bulk modulus. The Young's modulus is the most commonly used elastic modulus and is applicable to most materials. The shear modulus is used to measure the stiffness of materials in response to shear stress, and the bulk modulus is used to measure the stiffness of materials in response to hydrostatic pressure.

 
HOW IS ELASTICITY MODULUS CALCULATED?

The elastic modulus of a material can be calculated using the following equation:

Elastic modulus = stress / strain

where stress is the force applied to the material per unit area, and strain is the resulting deformation of the material. The elastic modulus is typically measured in units of pressure, such as megapascals (MPa) or gigapascals (GPa).

To measure the elastic modulus of a material, a sample of the material is subjected to a tensile or compressive load, and the resulting stress and strain are measured. The elastic modulus can then be calculated by dividing the stress by the strain.

In practice, the elastic modulus of a material is usually determined using a standard test procedure, such as the tensile test or the compression test. These tests involve applying a load to a sample of the material and measuring the resulting deformation. The elastic modulus can then be calculated from the measured stress and strain values.

It is important to note that the elastic modulus of a material can vary depending on the temperature, humidity, and other environmental conditions. In addition, the elastic modulus can vary depending on the type of loading that is applied to the material, such as tensile, compressive, or shear stress. Therefore, it is important to carefully control the test conditions when measuring the elastic modulus of a material.

HOW CAN ELASTICITY MODULUS BE IMPROVED?

There are several ways to improve the elastic modulus of composite panels:

  1. Use high-modulus fibers: The elastic modulus of a composite panel is largely determined by the modulus of the fibers used in the panel. Using high-modulus fibers, such as carbon fibers or high-strength fibers, can significantly increase the elastic modulus of the composite panel.

  2. Increase the fiber volume fraction: The elastic modulus of a composite panel also depends on the volume fraction of fibers in the panel. Increasing the fiber volume fraction can increase the elastic modulus of the composite panel.

  3. Use a high-modulus matrix: The matrix material that surrounds the fibers in a composite panel can also affect the elastic modulus of the panel. Using a matrix material with a high modulus, such as an epoxy resin or a polyimide, can increase the elastic modulus of the composite panel.

  4. Use a unidirectional fiber orientation: The orientation of the fibers in a composite panel can also affect the elastic modulus. Using a unidirectional fiber orientation, where the fibers are aligned in a single direction, can increase the elastic modulus of the composite panel.

  5. Use a hybrid fiber configuration: Using a hybrid fiber configuration, where different types of fibers are used in different directions, can also improve the elastic modulus of a composite panel.

  6. Improve the fiber-matrix interface: The strength of the fiber-matrix interface can also affect the elastic modulus of a composite panel. Improving the fiber-matrix interface, such as by using a compatible matrix material or by optimizing the fiber treatment process, can increase the elastic modulus of the composite panel.

 

 

Details
Materials & Properties
Hits: 3415
Here is the details and structural properties of a Nomex core and Aluminum core composite panels. L direction, W direction core shear modules depends on the ribbon direction, Elasticity modules of the skin materials. Poisson's Ratio


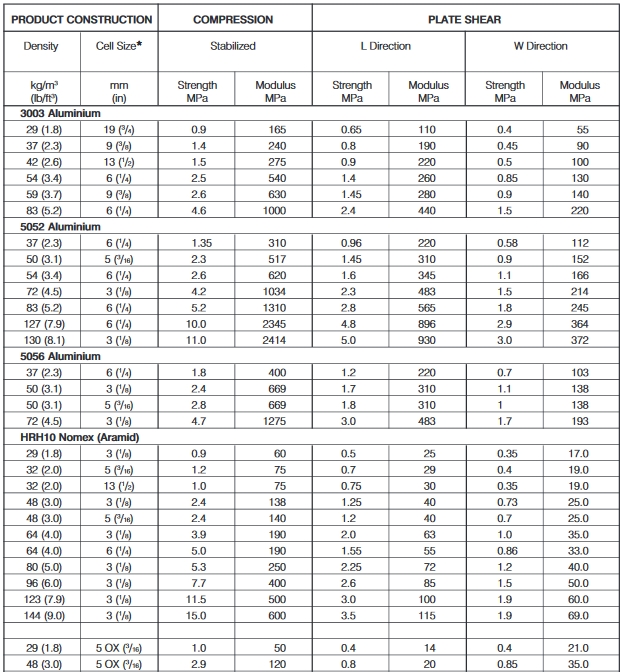
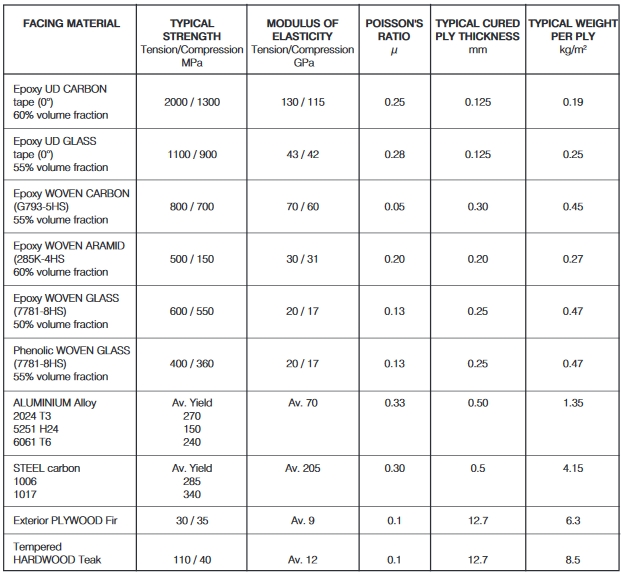
Source: http://www.hexcel.com/Resources/DataSheets/Brochure-Data-Sheets/Honeycomb_Sandwich_Design_Technology.pdf